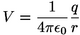
Twee hulpmiddelen om elektrische velden weer te geven zijn het tekenen van isopotentialen en veldlijnen. Met dit applet kunnen de isopotentialen en veldlijnen van puntladingen bestudeerd worden. Zo kan bijvoorbeeld het elektrisch veld van een dipool of quadrupool bestudeerd worden.
Op deze pagina:
Klik met de muis in het grijze vierkant om puntladingen toe te voegen: met de linkermuisknop krijg je een positief geladen deeltje en met de rechtermuisknop een negatief geladen deeltje. Als je op een puntlading klikt wordt deze geselecteerd en kun je hem met de muis verslepen. Van een geselecteerd deeltje kan rechts in beeld de lading en positie veranderd worden. Rechtsonder kun je de hoeveelheid getekende isopotentialen en veldlijnen veranderen.
Voor de elektrische potentiaal van een puntdeeltje geldt:
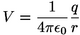
waarbij q de lading van het deeltje is en r de afstand tot het deeltje. Het elektrisch veld is hier minus de afgeleide van, en is dus
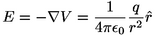
Voor meerdere puntdeeltjes is dit een kwestie van potentialen en elektrische velden optellen.
Een isopotentiaal is, zoals de naam al zegt, een oppervlak waarop de potentiaal overal hetzelfde is. In het geval van een tweedimensionale weergave zoals hierboven wordt dat dus een lijn. Bij één enkele puntlading zijn dit bolschillen of, geprojecteerd op twee dimensies, cirkels.
Een veldlijn is een lijn die overal de richting van het elektrisch veld volgt. Deze lijnen beginnen en eindigen alleen op ladingen of in het oneindige. De richting van het elektrisch veld is dus af te leiden uit de richting van de veldlijnen, maar ook de sterkte is met behulp van veldlijnen af te lezen. De grootte van het elektrisch veld is namelijk evenredig met de dichtheid van de lijnen. Dit heeft als gevolg dat het aantal lijnen wat uit een puntlading komt (of er in loopt, voor negatieve ladingen) evenredig is met de lading. Een puntlading met lading 2q heeft dus twee keer zoveel veldlijnen als een puntlading van q.
Het is belangrijk te beseffen dat de evenredigheid tussen veldlijnendichtheid en elektrisch veld geldt in drie dimensies. In twee dimensies, zoals hierboven, geldt dit niet en is de veldsterkte evenredig met de lijndichtheid in het kwadraat.
Wat opvalt is dat veldlijnen en isopotentialen altijd loodrecht op elkaar staan waar ze elkaar kruisen. Dit komt doordat isopotentialen in de richting lopen van de minste verandering van de potentiaal, terwijl veldlijnen in de richting lopen van de sterkste verandering van de potentiaal. Je kunt het vergelijken met een berglandschap, waarbij de hoogte evenredig is met de grootte van de potentiaal. Isopotentialen zijn paden die horizontaal lopen, bijvoorbeeld om een bergtop/positieve lading heen, terwijl veldlijnen zo steil mogelijk naar beneden lopen. Op het punt waar deze paden kruisen, staan ze altijd haaks op elkaar.
Dit applet benadert isopotentialen en veldlijnen. Met name voor veldlijnen kan dit zo nu en dan fouten opleveren. Zo kan het voorkomen dat het aantal veldlijnen per lading niet precies klopt, en ook kan de veldlijndichtheid soms afwijken van de aanwezige veldsterkte.